Structur2Vec+DQN[2017 ] Learning Combinatorial Optimization Algorithms over Graphs

This paper is 2017 NIPS. One of the improtant researchers is Bistra Dilkina, from USC.

Furthermore, existing works typically use the policy gradient for training [6], a method that is not particularly sample-efficient.

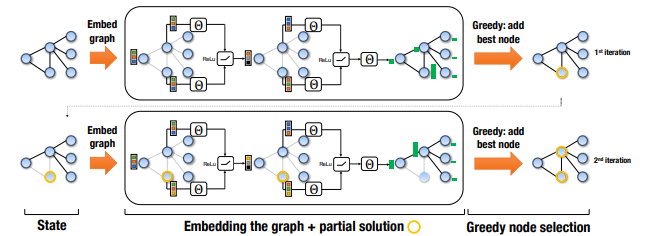
They used a single meta-learning algorithm, efficiently learns effective heuristics for each of the problems. They solve three problem: Minimum Vertex Cover (MVC), Maximum Cut (MAXCUT) and Traveling Salesman Problem (TSP). They use a greedy algorithm to solve the probem. A greedy algorithm will construct a solution by sequentially adding nodes to a partial solution S, based on maximizing some evaluation function Q that measures the quality of a node in the context of the current partial solution. A maintenance (or helper) procedure h(S) will be needed, which maps an ordered list S to a combinatorial structure satisfying the specific constraints of a problem. The quality of a partial solution S is given by an objective function $c(h(S), G)$based on the combinatorial structure $h$ of $S$.

A generic greedy algorithm selects a node v to add next such that v maximizes an evaluation
function,
$Q(h(S), v) \in\mathbb{ R}$, which depends on the combinatorial structure $h(S)$of the current
partial solution. Then, the partial solution
$S$ will be extended as

MVC: The helper function does not need to do any work, and $c(h(S), G) = -|S|$ The termination
criterion checks whether all edges have been covered.

MAXCUT: The helper function divides V into two sets, S and its complement $\bar{S} = V/S$, and maintains a cut-set $C = \{(u, v)|(u, v) \in E,u \in S, v\in\bar{S}\}$. Then, the cost is $c(h(S), G) =\sum_{(u, v)\in C}w(S(i), S(i+1))-w(S(|S|), S(1))$, and the termination criterion is activated when $S = V$ . Empirically, inserting a node u in the partial tour at the position which increases the tour length the least is a better choice. We adopt this insertion procedure as a helper
function for TSP

structure2vec

They used the idea of this paper

This graph embedding network will compute a p-dimensional feature embedding $µ_v$ for each node $v \in V$ , given the current partial solution $S$. One variant of the structure2vec architecture will initialize the embedding $µ^{(0)}_v$ at each node as 0, and for all $v \in V$ update the embeddings synchronously at each iteration as

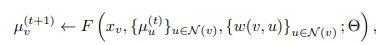
where $N (v)$ is the set of neighbors of node v in graph G, and F is a generic nonlinear mapping such as a neural network or kernel function.

Parameterizing Q function

design F to update a p-dimensional embedding $µ_v$ as

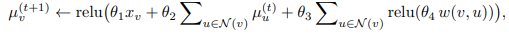
The summation over neighbors is one way of aggregating neighborhood information that is invariant to permutations over neighbors.

Once the embedding for each node is computed after T iterations, we will use these embeddings to define the $\hat{Q}(h(S), v;\Theta) = \theta_5^Trelu([\theta_6]\sum_{u\in V}\mu_u^{(T)}, \theta_7\mu_v^{(T)})$

$[·, ·]$ is the concatenation operator

Training RL

Actions: an action v is a node of G that is not part of the current state S. Similarly, we will represent actions as their corresponding p-dimensional node embedding µv, and such a definition is applicable across graphs of various sizes;

Rewards: the reward function $r(S, v)$ at state S is defined as the change in the cost function after
taking action v and transitioning to a new state
$S' := (S, v)$. That is

Policy: based on Qb, a deterministic greedy policy $\pi(v|S) := \argmax_{v'\in\bar{S}} \hat{Q}(h(S), v')$ will be
used.

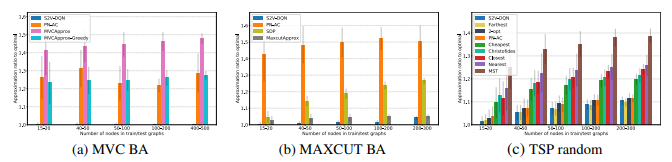
Experiment